三角形 内角 外角 328003-三角形 内角 外角 証明
今回の中2数学の解説は図形の合同から「三角形の内角・外角」についてです。 それぞれの用語や性質を確認し、練習問題を解いて理解を定着させましょう。 hissoritophysmathcom 今回は多角形です。 四角形以上の内角の考え方を確認していき 内角をそれぞれ 、 、 、外角を とします。 三角形の内角の和は であることから であり、この式を の形にすると ① となります。 次に直線のなす角が であることから であり、この式も の形にすると ② となります。(3) 正五角形では5つの外角の和は ゜だから1つの外角は ゜ したがって1つの内角は ゜です. 何角形でも外角の和は360° この問題は五角形の内角の和が540°になることを使っても求められるが,初めの2つの空欄を埋めるには,問題文で指定された順に答える方がよい.
中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su
三角形 内角 外角 証明
三角形 内角 外角 証明-動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 等号两边都减去∠1 也就变成了∠2∠3=∠4 由此我们也就得出了: 三角形的一个内角与它相邻的外角的和为180度 三角形的一个外角等于与它不相邻的两个内角的和 三角形的一个外角大于与它不相邻的任何一个内角 希望可以帮到你 9 已赞过 已踩过
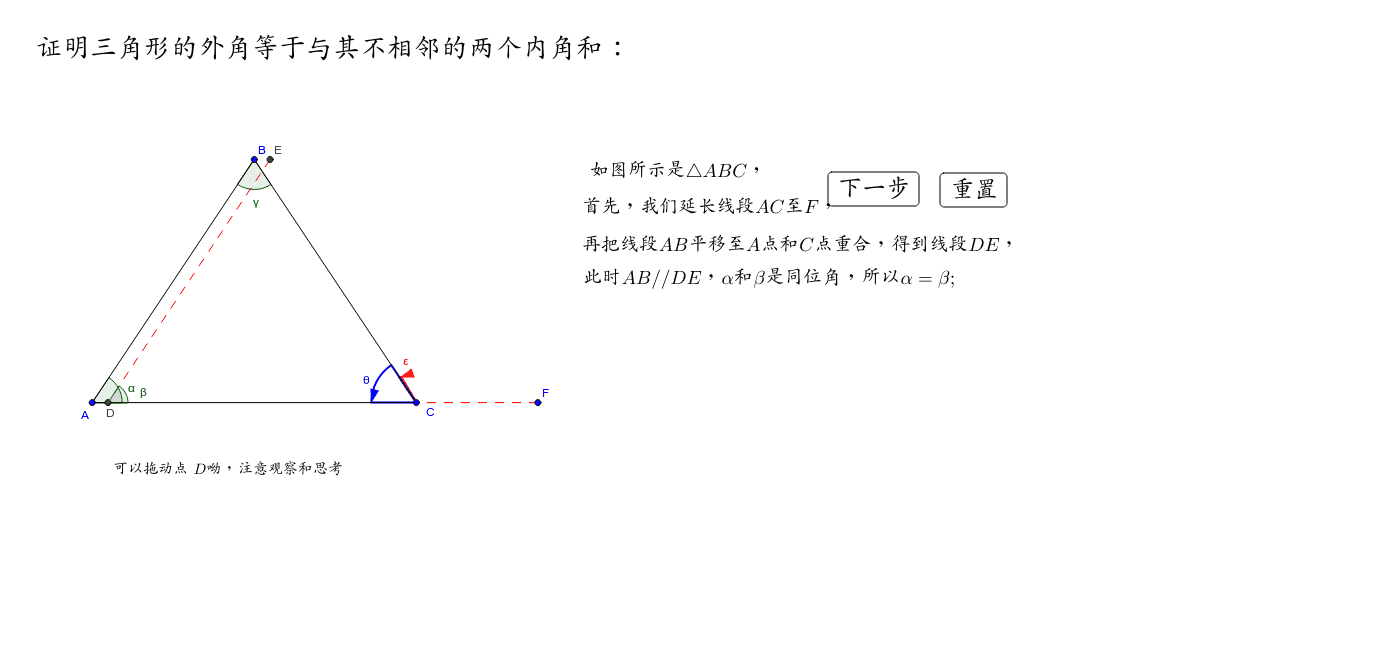



三角形的外角等于与其不相邻的两个内角之和 Geogebra
并且,三角形的一个外角等于不相邻的两个内角之和。 扩展资料 三角形内角和定理:三角形的内角和等于180°。 用数学符号表示为:在 ABC中,∠1∠2∠3=180°(见概述图)。 也可以用全称命题表示为:∀ ABC, ∠1∠2∠3=180°。 任意n边形内角和公式 任意n边形三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。三角形の外角の定理 『外角は、その外角のとなり以外の2つの内角の和に等しい』 つまり、下の図の通り。 外角の定理のひみつ外角= + ①三角形の内角の和は180度でした。 だから、
三角形・四角形の内角と外角 三角形、四角形の外角を知り、外角の和が360°を確認する ABCの外側にあるので ∠Cの外角 といいます。 まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 三角形の内角の和というのは,三角形の内側の角の大きさの和のことをいいます。 三角形の内角の和=180° 小学生女の子 三角形の内角・外角 中2数学 三角形の外角の定理については、意外と忘れられやすいのですが、とてもよく使いますし、便利なものなのでぜひ覚えておき、いつでも使えるようにしましょう。 また、今回のプリントは今後いろいろ応用を利かせる
外角定理(がいかくていり)とは、三角形の外角はそれと隣り合わない2つの内角の和に等しいということを示す、ユークリッド幾何学における定理。 その形状から、「スリッパの法則」と呼ばれることもある 要出典 。 証明内角と外角を足すと180°になる という特徴があります。 これを使って考えると 正多角形の内角1つ分の大きさは $$\large{180(外角)}$$ このように求めてやることができます。 正三角形の場合 复习与预习反馈:复习与预习反馈: 1 1三角形的内角和是三角形的内角和是 ; 2 2三角形的一个外角三角形的一个外角 与它不相邻的与它不相邻的 两个内角的和;两个内角的和; 3三角形的一个外角三角形的一个外角 任何一个与它任何一个与它 不相,新文库网xinwenkucom



头条问答 如何反驳学生认为三角形有六个外角 26个回答



三角形的外角等于与它不相邻的两个内角的和 Page18 浙教版八年级 初二 数学上册电子课本 教材 教科书 好多电子课本网
重点:三角形的外角及其性质 难点:运用三角形外角性质进行有关计算时能准确地表达推理的过程和方法。 三、教材分析: 教材由学生已经熟悉的三角形的内角和定理引入,然后探索三角形外角的性质。多角形の内角・外角③ 次の問いに答えなさい。 ⑴ 八角形の内角の和は何度か答えなさい。 ⑵ 正十二角形の1 つの外角の大きさは何度か答えなさい。 ⑶ 正十角形の1 つの内角の大きさは何度か答えなさい。 ポイント 多角形の内角の和:n 角形は(n−2) 個の三角形の合同 上の図ですと、オレンジ色の角度が外角、三角形の内側にあるのが外角です。 30 75 = 105 となります。 上の図の x の角度を求めなさい。 この問題では、「外角は隣にない2内角の和に等しい」というルールから、角 E の 40 ∘ と x の和の対象



有一个外角等于1 且有两个内角相等的三角形是 X题卡



三角形内角与外角的解题误区 5 4三角形的内角和 初中湘教版 数学中国网
三角形内角外角 与三角形有关的角 三角形的内角 内角三兄弟之争 在一个直角三角形里住着三个内角,平 时,它们三兄弟非常团结可是有一天,老二 突然不高兴,发起脾气来,它指着老大各頂角の内角と外角の和は180°ですので、三角形の場合、3つの内角を A, B, C としますと、外角の和が360°になるという式は、 ( 180 − A) ( 180 − B) ( 180 − C) = 360 となりますから、これを変形すると、 A B C = 180 が得られます。 ーーーーーーーーーーーー 右の にも内角の和が180° であることを利用して x = 180− 75 −35 = 70 x = 180 − 75 − 35 = 70 この問題は、内角と外角の関係を使っても使わなくても大して変わらないね よし、じゃあ次の問題 はかせちゃん 円周角の問題とかでもよく見る形なので はかせは蝶




教师资格证面试 小学数学真题教案设计 知乎



数学老师手抄版 初二数学 三角形内角与外角 经典题
三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます. 正三角形の1つの内角は60°、外角は1°なので、 外角の和は1°×3=360° 「あっ、そうそうそうそう、外角の和は360°だったね~」 と思い出そう!! 多角形の外角の和を忘れたら、正三角形で検証せよ!! 問題 図に示された角度は、全て三角形の外角だね?三角形の外角はそれととなり合わない2つの内角の和に等しいので ∠CBD = 41°17° = 58° x 41° 17° A D 50° 23° B C E 73° 58° x = 180° 58°73° = 49°




五边形内角和 五边形的内角和是多少度 52fmz购物网



三角形一个内角与一个外角的角平分线夹角的度数初中数学八年级上册 哔哩哔哩 Bilibili
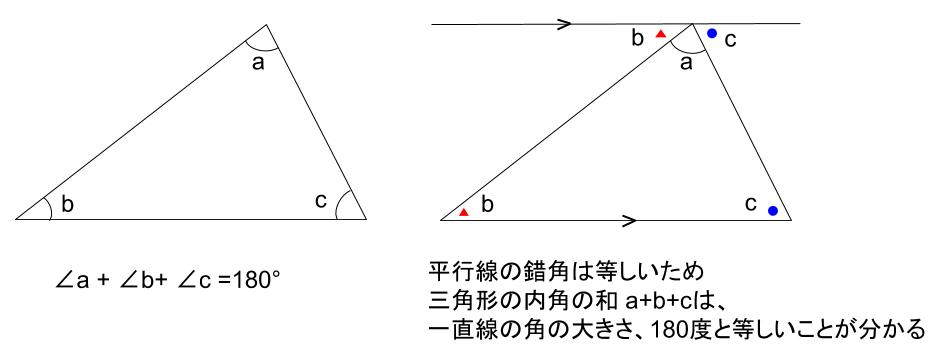
三角形の3つの内角の和は180°になる。 三角形の外角 内容 三角形の1つの外角は、そのとなりにない2つの内角の和に等しい。 証明a 図のように、 abcの辺bcを延長した直線上の点をdとする。 また、点cを通り辺baに平行な直線をceとする。




三角形内角外角平分线的夹角五个模型




五边形内角和 五边形的内角和是多少度 52fmz购物网
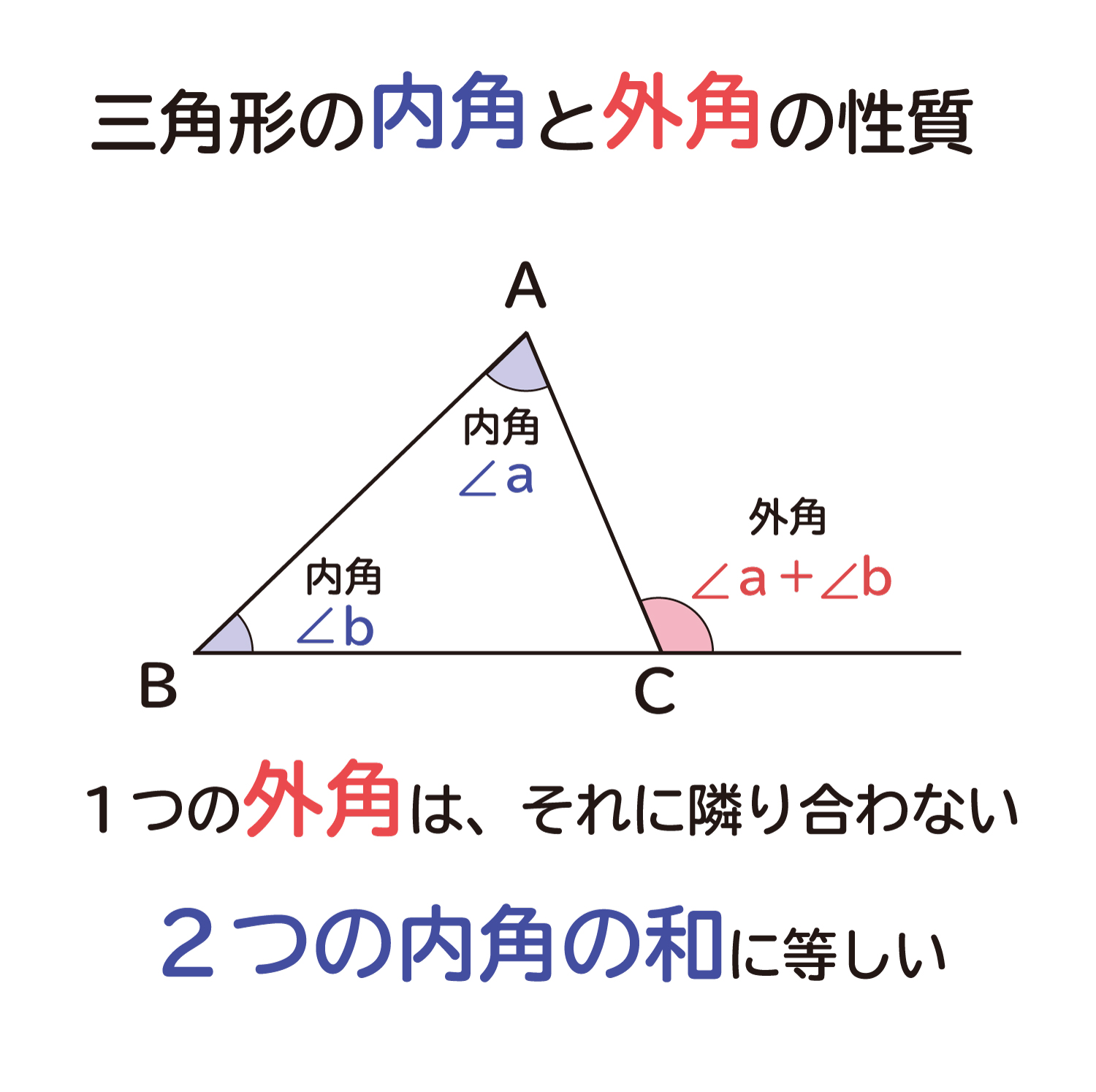



なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル



N边形的内角和计算公式 西瓜视频搜索




初一奥数第18讲三角形内角和经典例题 1 每日头条



Word版 巧用三角形的外角以及三角形内角和公式的变形来解决三角形中角的有关求解与证明 7 2与三角形有关的角 初中人教版 数学中国网




11 2 2三角形的外角 部编版八年级数学上册电子课本 易学啦




七年级数学多边形内角和与外角和 三角形 基础练习 文库吧



内角总和
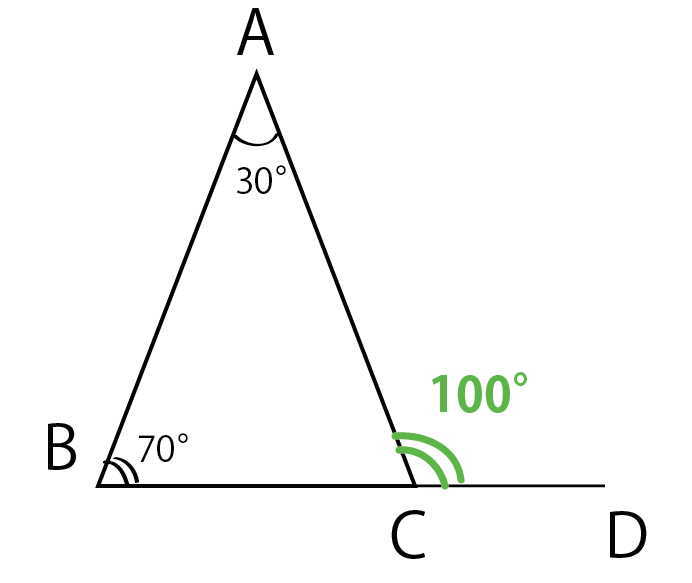



3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく
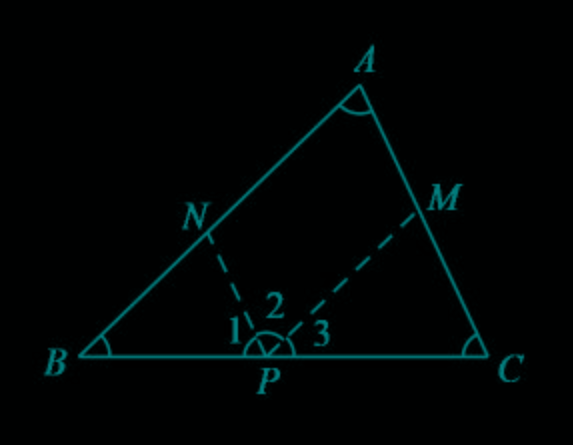



七下数学 三角形 内角和 外角 外角和定理 平行线




多边形的内角和与外角和 简书



七下数学 三角形 内角和 外角 外角和定理 平行线




中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su



三角形内角和是多少度 外角和度数是多少 初三网



三角形内角和是多少度 外角和度数是多少 初三网
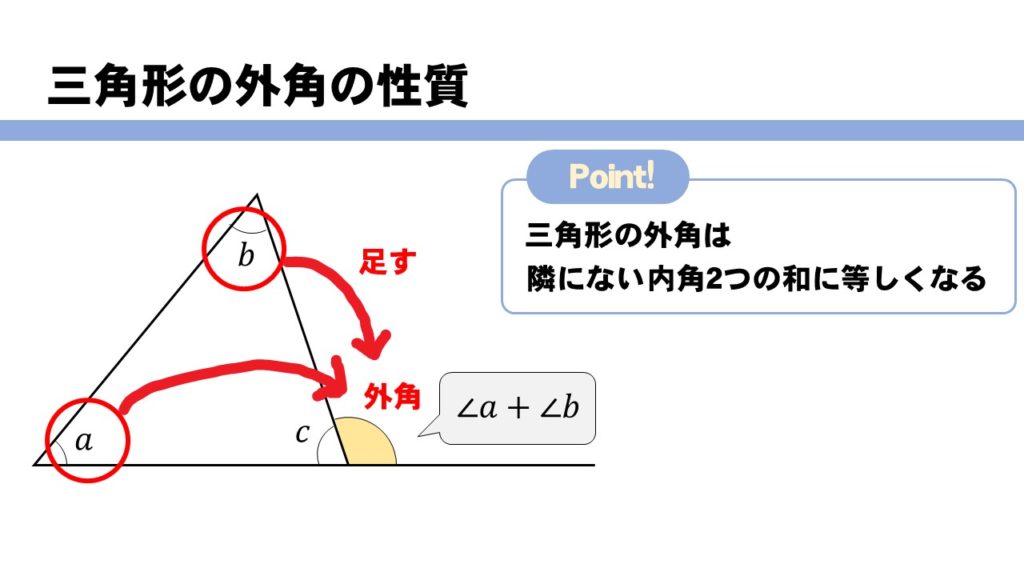



3分なるほど 三角形の内角 外角の性質について解説 数スタ




三角形内角和定理 平行线的证明ppt课件4 Ppt课件下载 人人ppt



As7kxbjad7ng6m




三角形的外角等于与其不相邻的两个内角之和 Geogebra




三角形内角和定理 平行线的证明ppt课件4下载 牛二ppt
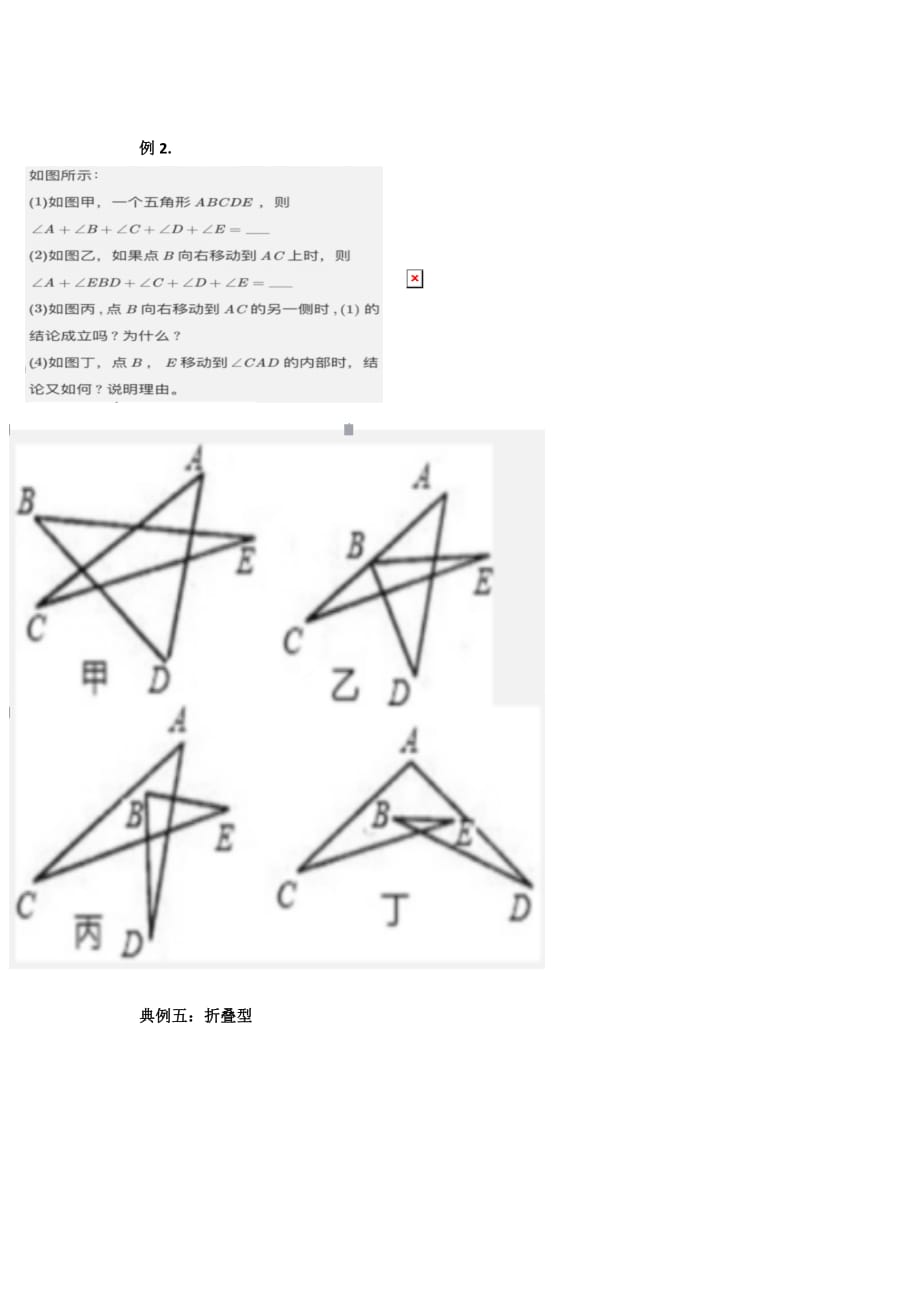



三角形内角与外角和典型例题 金锄头文库




三角形内角与外角和典型例题 金锄头文库




通俗数学 三角形外角和等于360 优胜于 内角和等于180



三角形有多少度 酷知经验网




多边形内角和与外角和的题型总结




初中数学 多边形的内角和与外角和题型总结 掌握这些就够了




内角和外角 维基百科 自由的百科全书



数学老师手抄版 初二数学 三角形内角与外角 经典题




3 三角形外角定理 简书



三角形的内角和外角 图片搜索
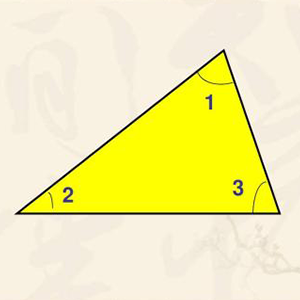



三角形内角和是多少度 搜狗指南
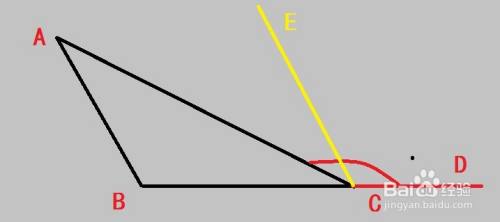



怎样证明三角形的外角大于任何一个不对应的内角 百度经验




七年级数学多边形内角和与外角和 三角形 基础练习 文库吧



正多边形内角和多边形内角和公式推导方法 尚书坊



探究与发现 探究一 我们知道 三角形的一个外角等于与它不相邻的两个内角的和 那么 三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢 已知 如图 Fdc 与 Ecd 分别为 Triangle Adc 的两个外角 试探究 A 与 Fdc Ecd 的




通俗数学 三角形外角和等于360 优胜于 内角和等于180



数学老师手抄版 初二数学 三角形内角与外角 经典题 三角形内角与外角 内角 外角 新浪新闻



三角形外角和公式



内角和外角图片 万图壁纸网



腾讯视频



内角的角度



三角形的外角 三角形ppt 第一ppt



三角形内角和是多少度 初三网



三角形的内角和定理 外角的性质 07年中考题集锦 7 2与三角形有关的角 初中人教版 数学中国网



三角形的外角1 主题阅读 我爱图谱 知识图谱 思维导图 Www 5itupu Com



1



利用三角形内角外角性质解决角度问题 哔哩哔哩 つロ干杯 Bilibili



头条问答 五边形内角和是多少 个回答



北师大版八年级上册 三角形内角和定理 外角 网易视频
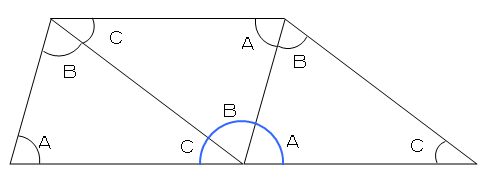



三角形の内角と外角の関係
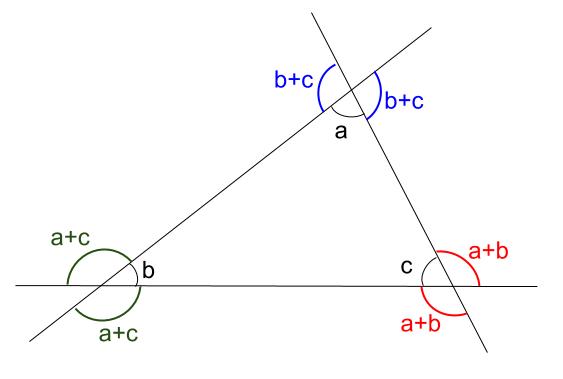



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




三角形内角外角定理多边形 三角形png图片素材免费下载 图片编号 Png素材网




11 2 2三角形外角 七年级上 数学 教案 优优课件



初一奧數第18講三角形內角和經典例題 3 雪花新闻
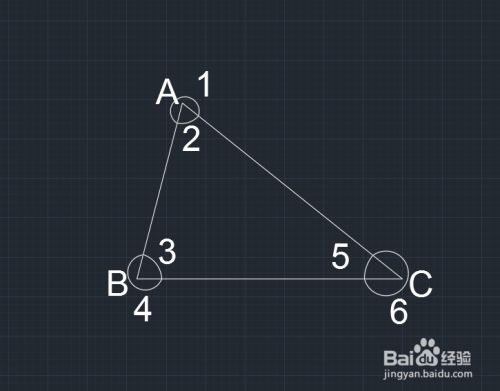



三角形外角和证明方法 百度经验




三角形的内角和外角 Ppt课件下载 牛二ppt



三角形的外角讲解 北京爱智康




多边形的内角和与外角和 简书
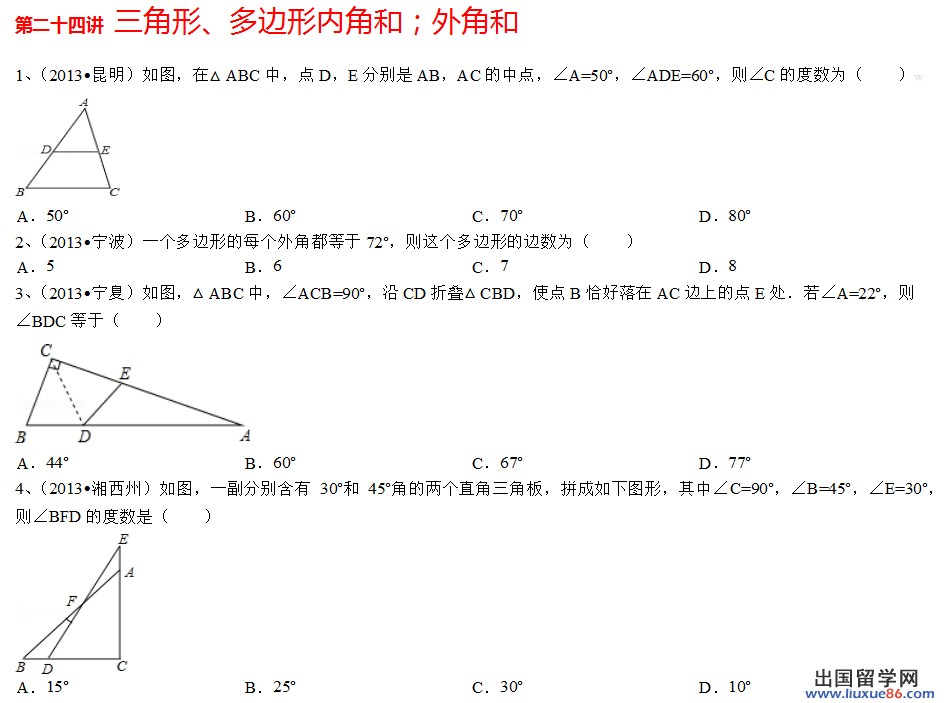



14初三数学三角形多边形内角和外角和



初一奧數第18講三角形內角和經典例題 2 雪花新闻




初中统考几何相似三角形 内角平分线与外角平分线的性质 老雷数学 Youtube




北师大版数学八年级上册 三角形外角定理的证明 Ppt课件1 Ppt 七彩学科网



三角形的外角 三角形ppt 第一ppt




外角定理外角定理 Kmbymh
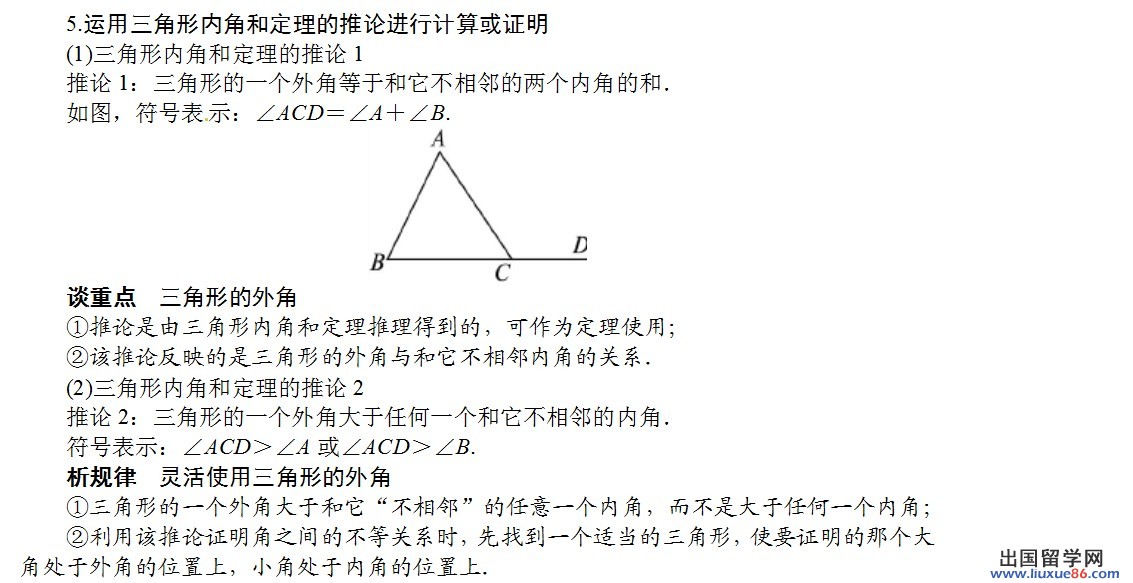



三角形内角和
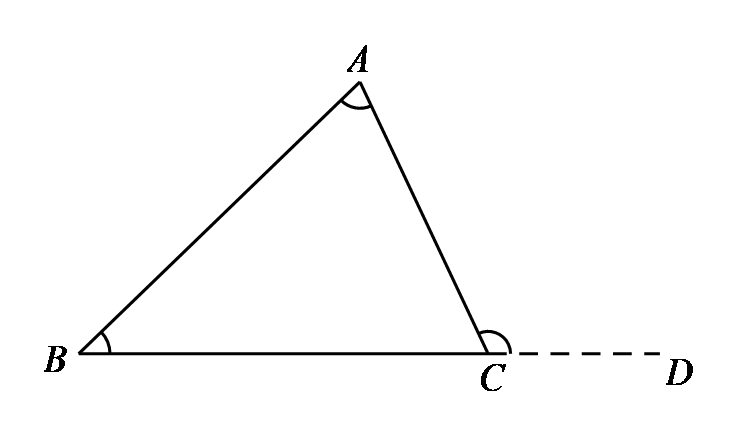



三角形内角和图片 搜狗图片搜索




多边形的内角



内角和外角图片 万图壁纸网




多边形的内角



三角形有多少度 酷知经验网



初中数学与三角形有关的角 掌握考点 明确考法 学会解题思路




数学 中2 48 三角形の内角と外角 基本編 Youtube



三角形内角和定理三角形的内角和定理是什么



三角形的外角说课稿 我的网站




三角形内角和定理 平行线的证明ppt课件4下载 牛二ppt




11 2 2 三角形的外角 导学案 Docx 三九文库网
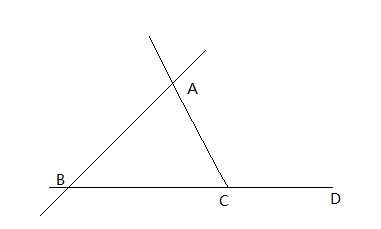



三角形的内角和推论8 Id拂晓犬吠 博客园
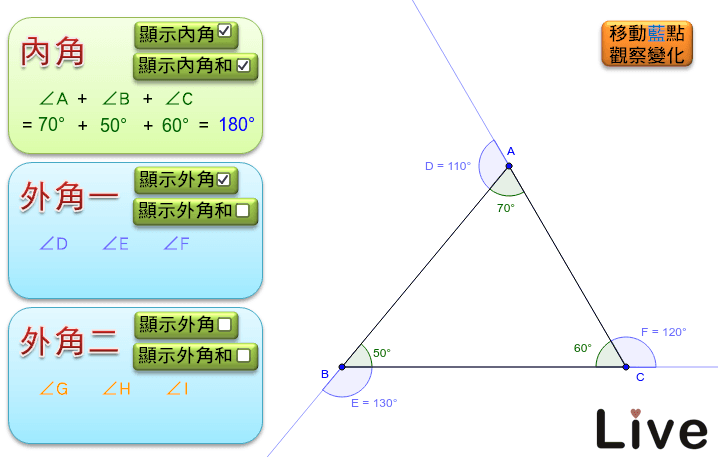



三角形的內角 外角 內角和與外角和 Geogebra




06三角形内角和定理的证明平行线的证明初中数学初二 Youtube




三角形内角和定理 平行线的证明ppt课件3 Ppt课件下载 人人ppt




File 三角形の内角と外角 Png 维基百科 自由的百科全书




如何找到三角形的外角 数学21



2 三角形的内角与外角和 Page76 华师大版七年级数学下册电子课本 教材 教科书 好多电子课本网
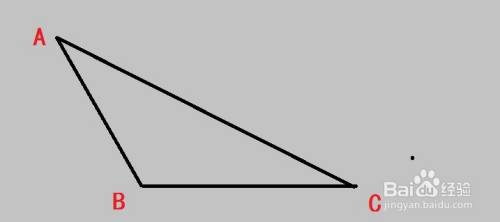



怎样证明三角形的外角大于任何一个不对应的内角 百度经验



三角形内角和定理 平行线的证明ppt 第2课时 第一ppt




三角形内角和外角和 三角形内角和外角和 三人行教育网 Www 3rxing Org



数学老师手抄版 初二数学 三角形内角与外角 经典题



三角形的内角与外角会怎么考 老教师说有四个常考题




外角和与内角和 哔哩哔哩




三角形内角外角平分线的夹角五个模型




内角和外角 Wikiwand
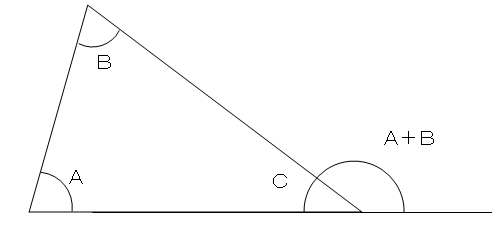



三角形の内角と外角の関係




5 5 三角形内角和定理 初中电子课本



11 2 2 三角形的外角 人教版八年级上册数学电子课本 数九网
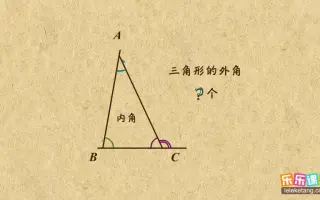



三角形的内角和外角 搜索结果 哔哩哔哩 Bilibili
コメント
コメントを投稿